Waveguide with Dispersion

In this chapter, we’ll extend our waveguide model to include dispersion effects. We’ll see how to model wavelength-dependent behavior in optical waveguides.

Waveguide Model with 1st-order Dispersion

Parameters:

• \(\lambda\): Wavelength (µm)

• \(\lambda_0\): Reference wavelength (µm)

• \(n_{\text{eff}}\): Effective index at \(\lambda_0\)

• \(n_g\): Group index

• \(L\): Waveguide length (µm)

• \(\alpha\): Propagation loss (dB/cm)

Effective index with dispersion:

\[\large \tilde{n}_{\text{eff}}(\lambda) = \underbrace{n_{\text{eff}}}_{\text{reference index}} - \underbrace{(\lambda - \lambda_0) \cdot \frac{n_g - n_{\text{eff}}}{\lambda_0}}_{\text{dispersion term}}\]

Transmission:

\[\large T(\lambda) = \underbrace{10^{-\frac{\alpha L}{20}}}_{\text{amplitude}} \cdot \underbrace{e^{i \frac{2\pi \tilde{n}_{\text{eff}}(\lambda) L}{\lambda}}}_{\text{phase with dispersion}}\]

import jax.numpy as jnp
from rich import print as rprint
import sax


def waveguide_1st_order_dispersion(
    wl: float = 1.55,
    wl0: float = 1.55,
    neff: float = 2.34,
    ng: float = 3.4,
    length: float = 10.0,
    loss_db_per_cm: float = 0.5,
) -> sax.SDict:
    """A simple straight waveguide model.

    Args:
        wl: wavelength in microns.
        wl0: reference wavelength in microns.
        neff: effective index.
        ng: group index.
        length: length of the waveguide in microns.
        loss_db_per_cm: loss in dB/cm.

    """
    dwl = wl - wl0
    dneff_dwl = (ng - neff) / wl0
    _neff = neff - dwl * dneff_dwl
    loss_db_per_µm = loss_db_per_cm * 1e-4
    phase = 2 * jnp.pi * _neff * length / wl
    amplitude = jnp.asarray(10 ** (-loss_db_per_µm * length / 20), dtype=complex)
    transmission = amplitude * jnp.exp(1j * phase)
    return sax.reciprocal(
        {
            ("o1", "o2"): transmission,
        }
    )

rprint(waveguide_1st_order_dispersion())
rprint(waveguide_1st_order_dispersion(wl=1.6))

{
    ('o1', 'o2'): Array(0.8207162+0.57123533j, dtype=complex128),
    ('o2', 'o1'): Array(0.8207162+0.57123533j, dtype=complex128)
}

{
    ('o1', 'o2'): Array(-0.84859541+0.52893356j, dtype=complex128),
    ('o2', 'o1'): Array(-0.84859541+0.52893356j, dtype=complex128)
}

Note that we used sax.reciprocal to simplify the code, since we have S21 = S12.

Waveguide Model with Generalized Dispersion

import jax
import jax.numpy as jnp
import xarray as xr
import sax
from jaxtyping import Array, ArrayLike
from jax import grad


def _interpolate_neff(xarr: xr.DataArray, **kwargs: ArrayLike) -> jnp.ndarray:
    # Extract interpolation dims from xarray
    dims = [d for d in xarr.coords if d != "neff_te0"]

    # Ensure required args are provided
    missing = [d for d in dims if d not in kwargs]
    if missing:
        raise ValueError(f"Missing required interpolation inputs: {missing}")

    # Broadcast all input arrays
    arrays = [jnp.asarray(kwargs[dim]) for dim in dims]
    broadcasted = jnp.broadcast_arrays(*arrays)
    shape = broadcasted[0].shape

    # Prepare kwargs for interpolation
    interp_args = {dim: arr.ravel() for dim, arr in zip(dims, broadcasted, strict=True)}

    # Interpolate
    result = sax.interpolate_xarray(xarr, **interp_args)["neff_te0"]
    return result.reshape(shape)


with jax.ensure_compile_time_eval():
    xarr = (
        xr.open_dataarray("data/neff_te0.nc")
        .load()
        .expand_dims({"neff_te0": ["neff_te0"]}, -1)
    )

# @jax.jit
def waveguide_generalized_dispersion(
    wl: float,
    length: float = 10.0,
    loss_db_per_cm: float = 0.5,
) -> sax.SDict:
    """Waveguide with interpolated neff."""

    neff = _interpolate_neff(
        xarr=xarr,
        wavelength=wl,
    )
    loss_db_per_µm = loss_db_per_cm * 1e-4
    phase = 2 * jnp.pi * neff * length / wl
    amplitude = jnp.asarray(10 ** (-loss_db_per_µm * length / 20), dtype=complex)
    transmission = amplitude * jnp.exp(1j * phase)

    return sax.reciprocal({("o1", "o2"): transmission})

waveguide_generalized_dispersion(1.55)

{('o1', 'o2'): Array(0.89962731-0.43652672j, dtype=complex128),
 ('o2', 'o1'): Array(0.89962731-0.43652672j, dtype=complex128)}

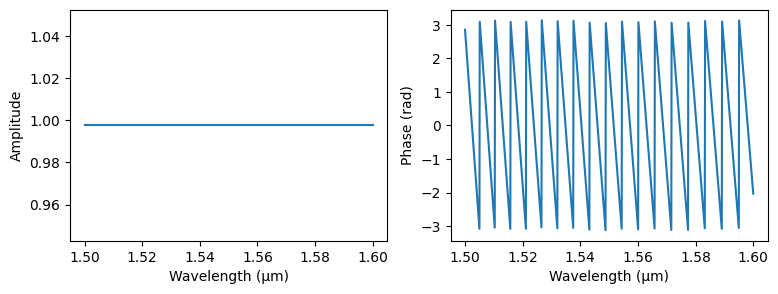
import matplotlib.pyplot as plt

wls = jnp.linspace(1.5, 1.6, 1000)
transmission = waveguide_generalized_dispersion(wl=wls, length=100.0, loss_db_per_cm=1)
s21 = transmission[("o1", "o2")]

plt.figure(figsize=(9, 3))
plt.subplot(1, 2, 1)
plt.plot(wls, jnp.abs(s21)**2)
plt.xlabel("Wavelength (µm)")
plt.ylabel("Amplitude")
plt.subplot(1, 2, 2)
plt.plot(wls, jnp.angle(s21))
plt.xlabel("Wavelength (µm)")
plt.ylabel("Phase (rad)")
plt.show()