CMT: Intro#
In this chapter (as well as the next two chapters) we develop semi-analytical models based on coupled mode theory discussed in this paper: Design Space Exploration of Microring Resonators in Silicon Photonic Interconnects: Impact of the Ring Curvature
(Another good read for a simpler case is Evanescent waveguide couplers)
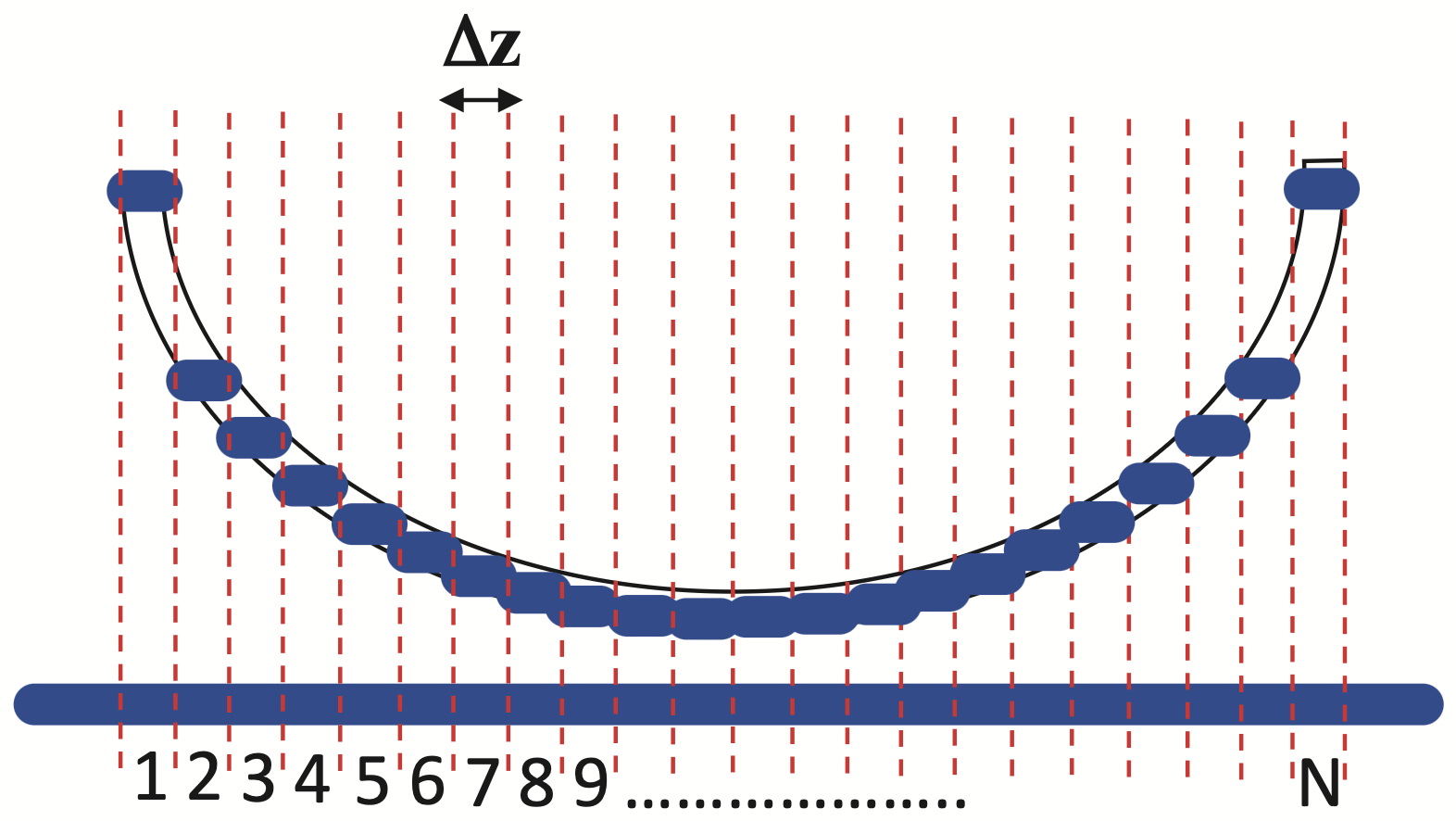
The main idea is to discretize the coupling area into many sections, each approximated as a simple directional coupler with a fixed gap:
Imports#
import doModels.RefractiveIndex as ri
import doModels.fem as fem
import doModels.SemiAnalyticalCouplers as analyze
import matplotlib.pyplot as plt
import numpy as np
import xarray as xr
from datetime import datetime
from tqdm.notebook import tqdm
Define Stack#
stack = fem.CoupledWaveguides(gap=0.2,
w_core_1=0.45,
w_core_2=0.45,
h_core=0.22,
n_clad_func=ri.silica,
n_core_func=ri.silicon)
Database of Coupled Waveguides#
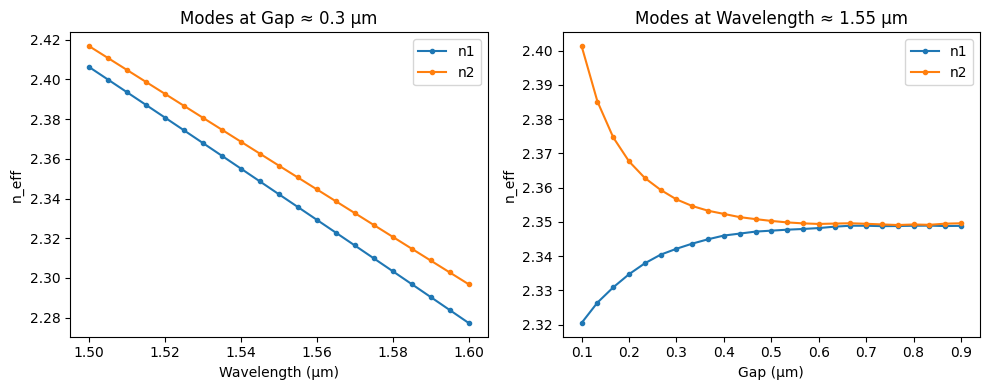
First, we create a database of super-modes for two adjacent waveguides whilst sweeping gap and wavelength. We use FEMWELL as described in Chapter 5. We store the results in an xarray netcdf file.
num_modes = 2
_gap = np.linspace(0.1, 0.9, 25)
_wavelength = np.arange(1.5, 1.6, 0.005)
n = np.zeros((num_modes, len(_gap), len(_wavelength)))
for i, gap in enumerate(tqdm(_gap)):
for j, wavelength in enumerate(_wavelength):
stack.gap = gap
modes = fem.supermode_solver(
coupled_waveguides=stack,
wavelength=wavelength,
num_modes=num_modes,
resolution=0.02,
)
n[:, i, j] = modes
ds = xr.Dataset(
{
f"n{k+1}": (["gap", "wavelength"], n[k, :, :])
for k in range(num_modes)
},
coords={"gap": _gap, "wavelength": _wavelength},
)
ds_sorted = analyze.adiabatic_mode_tracker1(ds)
ds_sorted.to_netcdf("data/coupled_wgs.nc")
print(ds)
<xarray.Dataset> Size: 9kB
Dimensions: (gap: 25, wavelength: 21)
Coordinates:
* gap (gap) float64 200B 0.1 0.1333 0.1667 0.2 ... 0.8333 0.8667 0.9
* wavelength (wavelength) float64 168B 1.5 1.505 1.51 ... 1.59 1.595 1.6
Data variables:
n1 (gap, wavelength) float64 4kB 2.454 2.449 2.443 ... 2.294 2.286
n2 (gap, wavelength) float64 4kB 2.388 2.381 2.374 ... 2.293 2.287
Load Database#
ds = xr.load_dataset("data/coupled_wgs.nc")
analyze.plot_interpolated_modes(ds, wl=1.55, gap=0.3)
Exponential Fit#
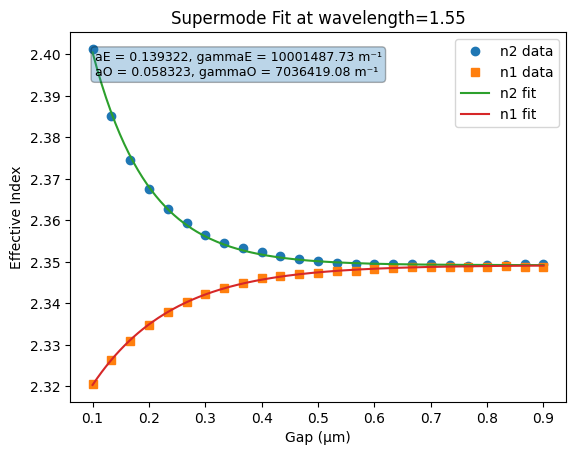
In the paper we cited above, the authors make a few geometrical arguments and apply some approximations to come up with a closed form expression for coupling coefficients of the directional coupler (See Eq. 11). One is to assume the indices of these supermodes follow an exponential as a function of gap:
aE, gammaE, aO, gammaO = analyze.fit_supermodes(ds,
interp_at={"wavelength":1.55},
plot=True)
Compute Coupling Coefficient#
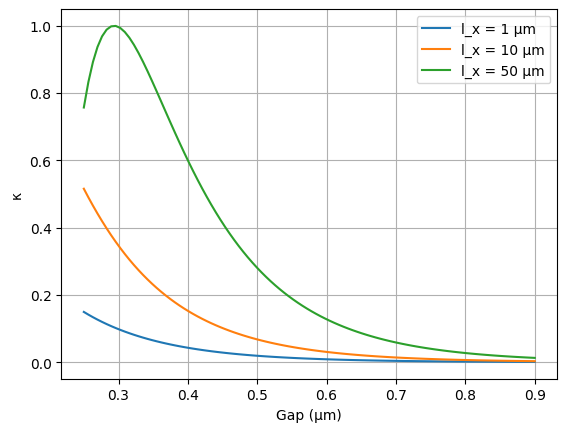
Following Eq. 11, we compute the coupling coefficient \(\kappa\) as a function of gap, wavelength, and length.
Show code cell source
# --- Plot κ vs gap ---
lambda_µm = 1.55
gaps_µm = np.linspace(0.250, 0.9, 100)
lengths_µm = [1, 10, 50]
kappa_results = np.zeros((len(lengths_µm), len(gaps_µm)))
fit_params = {}
fit_params['aE'], fit_params['gammaE'], fit_params['aO'], fit_params['gammaO'] = analyze.fit_supermodes(ds, interp_at={"wavelength":lambda_µm})
for i, length_x_µm in enumerate(lengths_µm):
for j, d in enumerate(gaps_µm):
kappa_results[i, j] = analyze.kappa_directional_coupler(gap_µm=d,
R_µm=20,
lambda_µm=lambda_µm,
length_x_µm=length_x_µm,
v_offset_µm=15,
fit_params=fit_params,
wg_width_µm=stack.w_core_1)
plt.figure()
for i, length_x_µm in enumerate(lengths_µm):
plt.plot(gaps_µm, kappa_results[i], label=f'l_x = {length_x_µm} µm')
plt.xlabel('Gap (µm)')
plt.ylabel('κ')
plt.grid(True)
plt.legend()
# --- Plot κ vs wavelength for fixed gaps ---
wavelengths_µm = np.linspace(1.50, 1.599, 100)
fixed_gaps = [0.3, 0.4, 0.5]
plt.figure()
for d in fixed_gaps:
kappa_vals = []
for λ in wavelengths_µm:
params = analyze.fit_supermodes(ds, interp_at={"wavelength": λ}, plot=False)
kappa = analyze.kappa_directional_coupler(gap_µm=d,
R_µm=20,
lambda_µm=λ,
length_x_µm=10, # or any fixed length
v_offset_µm=15,
fit_params=dict(zip(['aE', 'gammaE', 'aO', 'gammaO'], params)),
wg_width_µm=stack.w_core_1)
kappa_vals.append(kappa)
plt.plot(wavelengths_µm, kappa_vals, label=f'gap = {d} µm')
plt.xlabel('Wavelength (µm)')
plt.ylabel('κ')
plt.grid(True)
plt.legend()
<matplotlib.legend.Legend at 0x11c4de8d0>
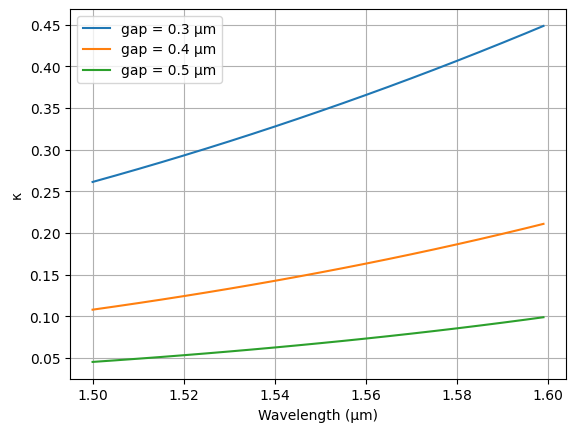
To better visualize the coupling coefficient, we precomputed it for a range of parameters (gap, radius, length_x, and v_offset, wavelength) and store them in a look-up table. This is the simplest way to create an interactive plot shown in the next page.
Show code cell source
# Define ranges
gap_vals = np.arange(0.25, 0.9, 0.04) # gaps in µm
radius_vals = np.arange(5, 100, 20) # radii in µm
wavelengths = np.arange(1.5, 1.6 , 0.005) # wavelengths in µm
length_x_vals = np.arange(0, 100, 8)
v_offset_vals = np.arange(5, 100, 40)
# Initialize array
kappa_array = np.zeros((len(wavelengths), len(gap_vals), len(radius_vals), len(length_x_vals), len(v_offset_vals)))
for i0, wl in enumerate(wavelengths):
fit_params = {}
fit_params['aE'], fit_params['gammaE'], fit_params['aO'], fit_params['gammaO'] = analyze.fit_supermodes(ds_sorted, interp_at={"wavelength":wl})
for i1, gap in enumerate(gap_vals):
for i2, radius in enumerate(radius_vals):
for i3, length_x in enumerate(length_x_vals):
for i4, v_offset in enumerate(v_offset_vals):
kappa_array[i0, i1, i2, i3, i4] = analyze.kappa_directional_coupler(gap_µm=gap,
R_µm=radius,
lambda_µm=wl,
length_x_µm=length_x,
v_offset_µm=v_offset,
fit_params=fit_params,
wg_width_µm=stack.w_core_1)
if np.isnan(kappa_array[i0, i1, i2, i3, i4]):
print(gap, radius, wl, length_x)
xarr_out = xr.DataArray(
data=kappa_array,
coords={
"wavelength": wavelengths,
"gap": gap_vals,
"radius": radius_vals,
"length_x": length_x_vals,
"v_offset": v_offset_vals,
},
dims=["wavelength", "gap", "radius", "length_x", "v_offset"],
name="kappa"
)
xarr_out.to_netcdf("data/directional_coupler.nc")
xarr_out.to_dataframe().reset_index().to_json("data/directional_coupler.json", orient="records")