Dispersion: Symbolic Regression#
import matplotlib.pyplot as plt
import numpy as np
import xarray as xr
ds = xr.load_dataset("data/neff_te0_db.nc")
print(ds)
<xarray.Dataset> Size: 10kB
Dimensions: (wavelength: 61, top_width: 20)
Coordinates:
* wavelength (wavelength) float64 488B 1.4 1.405 1.41 ... 1.69 1.695 1.7
* top_width (top_width) float64 160B 0.3 0.32 0.34 0.36 ... 0.64 0.66 0.68
Data variables:
neff_te0 (top_width, wavelength) float64 10kB 2.036 2.027 ... 2.463 2.459
wavelengths = ds["wavelength"].values
top_widths = ds["top_width"].values
neff = ds["neff_te0"].values
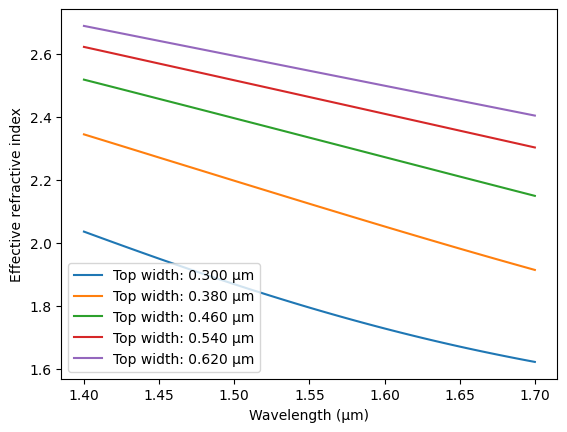
plt.figure()
plt.xlabel("Wavelength (µm)")
plt.ylabel("Effective refractive index")
for i in range(0, len(top_widths), 4):
plt.plot(wavelengths, neff[i], label=f"Top width: {top_widths[i]:.3f} µm")
plt.legend()
plt.show()
Symbolic Regression#
import numpy as np
from pysr import PySRRegressor
import xarray as xr
from itertools import product
from sklearn.preprocessing import StandardScaler
import matplotlib.pyplot as plt
from sklearn.metrics import r2_score, mean_squared_error
from matplotlib import pyplot as plt
ds = xr.load_dataset("data/neff_te0_db.nc")
coord_names = ["top_width", "wavelength"]
coords = [ds.coords[name].values for name in coord_names]
X = np.array(list(product(*coords)))
y = ds["neff_te0"].values.flatten()
# Normalize features
scaler_X = StandardScaler()
X_scaled = scaler_X.fit_transform(X)
scaler_y = StandardScaler()
y_scaled = scaler_y.fit_transform(y.reshape(-1, 1)).flatten()
model = PySRRegressor(
niterations=400,
populations=40,
maxsize=40,
verbosity=0
)
model.fit(X_scaled, y_scaled)
Detected IPython. Loading juliacall extension. See https://juliapy.github.io/PythonCall.jl/stable/compat/#IPython
/Users/vahid/doplaydo/doModels/.venv/lib/python3.12/site-packages/pysr/sr.py:2811: UserWarning: Note: it looks like you are running in Jupyter. The progress bar will be turned off.
warnings.warn(
PySRRegressor.equations_ = [ pick score equation \ 0 0.000000e+00 x0 1 3.201563e-02 x0 * 0.87595063 2 5.158965e-01 (x1 * -0.40640774) + x0 3 1.026243e-01 (x0 * 0.87594867) - (x1 * 0.40640372) 4 7.402805e-08 ((-1.6106493e-7 - x0) * -0.8759514) - (x1 * 0.... 5 7.478727e-01 ((x1 + ((x0 + -2.515248) * x0)) - 0.99999523) ... 6 6.264657e-01 (((x1 * -0.41697693) + x0) + 0.27268115) * ((x... 7 2.596142e-01 (((x0 * -0.2750113) + 1.593463) * (x0 + (2.609... 8 4.555390e-01 (x0 - (((x0 * 0.07233008) - 0.40601394) * ((((... 9 1.738736e-02 ((x0 * 1.1750462) - (((x0 * 0.0703593) - 0.406... 10 2.600872e-01 ((-0.35148537 - (((x0 * (x0 * -0.67813367)) - ... 11 1.533204e-03 ((-0.32173187 - ((((-0.72107697 * x0) * (x0 - ... 12 7.522903e-02 ((-0.3548211 - (((((x0 * (x0 * (x1 * 0.0083031... 13 1.416884e-01 ((-0.35471416 - (((x0 * (-0.11471766 + (x1 * (... 14 >>>> 1.365409e-01 ((-0.31943703 - ((((x0 * -0.73160255) * (x0 - ... 15 3.477136e-02 ((-0.61338526 - (((((((x0 * x1) * 0.014427088)... 16 3.509060e-02 (((-0.8608156 - x0) - (((((((x0 * 0.020068347)... 17 6.168531e-02 (((-0.871374 - x0) - ((((x0 * (x0 - -0.5435605... 18 1.059197e-02 (((-0.86151135 - x0) - ((((((x0 + -0.19577916)... loss complexity 0 0.248098 1 1 0.232709 3 2 0.082930 5 3 0.067542 7 4 0.067542 9 5 0.015135 11 6 0.004324 13 7 0.002572 15 8 0.000416 19 9 0.000402 21 10 0.000239 23 11 0.000238 25 12 0.000205 27 13 0.000154 29 14 0.000117 31 15 0.000110 33 16 0.000102 35 17 0.000090 37 18 0.000088 39 ]In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
Parameters
| model_selection | 'best' | |
| binary_operators | None | |
| unary_operators | None | |
| expression_spec | None | |
| niterations | 400 | |
| populations | 40 | |
| population_size | 27 | |
| max_evals | None | |
| maxsize | 40 | |
| maxdepth | None | |
| warmup_maxsize_by | None | |
| timeout_in_seconds | None | |
| constraints | None | |
| nested_constraints | None | |
| elementwise_loss | None | |
| loss_function | None | |
| loss_function_expression | None | |
| loss_scale | 'log' | |
| complexity_of_operators | None | |
| complexity_of_constants | None | |
| complexity_of_variables | None | |
| complexity_mapping | None | |
| parsimony | 0.0 | |
| dimensional_constraint_penalty | None | |
| dimensionless_constants_only | False | |
| use_frequency | True | |
| use_frequency_in_tournament | True | |
| adaptive_parsimony_scaling | 1040.0 | |
| alpha | 3.17 | |
| annealing | False | |
| early_stop_condition | None | |
| ncycles_per_iteration | 380 | |
| fraction_replaced | 0.00036 | |
| fraction_replaced_hof | 0.0614 | |
| weight_add_node | 2.47 | |
| weight_insert_node | 0.0112 | |
| weight_delete_node | 0.87 | |
| weight_do_nothing | 0.273 | |
| weight_mutate_constant | 0.0346 | |
| weight_mutate_operator | 0.293 | |
| weight_swap_operands | 0.198 | |
| weight_rotate_tree | 4.26 | |
| weight_randomize | 0.000502 | |
| weight_simplify | 0.00209 | |
| weight_optimize | 0.0 | |
| crossover_probability | 0.0259 | |
| skip_mutation_failures | True | |
| migration | True | |
| hof_migration | True | |
| topn | 12 | |
| should_simplify | True | |
| should_optimize_constants | True | |
| optimizer_algorithm | 'BFGS' | |
| optimizer_nrestarts | 2 | |
| optimizer_f_calls_limit | None | |
| optimize_probability | 0.14 | |
| optimizer_iterations | 8 | |
| perturbation_factor | 0.129 | |
| probability_negate_constant | 0.00743 | |
| tournament_selection_n | 15 | |
| tournament_selection_p | 0.982 | |
| parallelism | None | |
| procs | None | |
| cluster_manager | None | |
| heap_size_hint_in_bytes | None | |
| batching | False | |
| batch_size | 50 | |
| fast_cycle | False | |
| turbo | False | |
| bumper | False | |
| precision | 32 | |
| autodiff_backend | None | |
| random_state | None | |
| deterministic | False | |
| warm_start | False | |
| verbosity | 0 | |
| update_verbosity | None | |
| print_precision | 5 | |
| progress | True | |
| logger_spec | None | |
| input_stream | 'stdin' | |
| run_id | None | |
| output_directory | None | |
| temp_equation_file | False | |
| tempdir | None | |
| delete_tempfiles | True | |
| update | False | |
| output_jax_format | False | |
| output_torch_format | False | |
| extra_sympy_mappings | None | |
| extra_torch_mappings | None | |
| extra_jax_mappings | None | |
| denoise | False | |
| select_k_features | None |
Show code cell source
# Get all equations and their metrics
equations_df = model.equations_
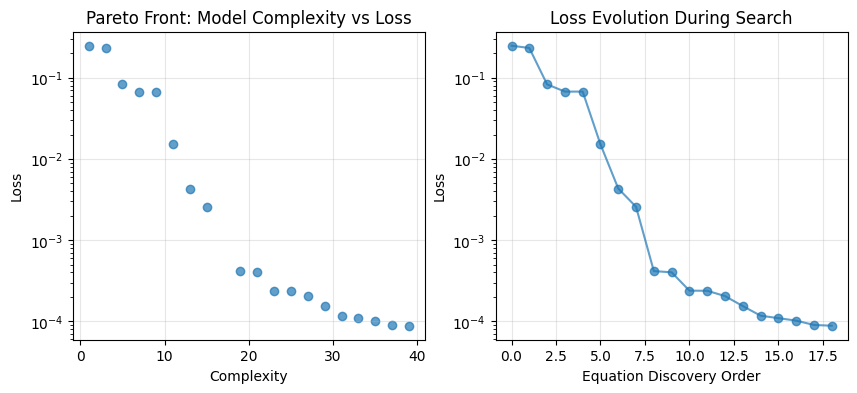
# Plot complexity vs loss (Pareto front)
plt.figure(figsize=(10, 4))
plt.subplot(1,2,1)
plt.scatter(equations_df['complexity'], equations_df['loss'], alpha=0.7)
plt.xlabel('Complexity')
plt.ylabel('Loss')
plt.title('Pareto Front: Model Complexity vs Loss')
plt.yscale('log') # Often helpful since loss can vary by orders of magnitude
plt.grid(True, alpha=0.3)
# Plot loss vs equation index (discovery order)
plt.subplot(1,2,2)
plt.plot(equations_df.index, equations_df['loss'], 'o-', alpha=0.7)
plt.xlabel('Equation Discovery Order')
plt.ylabel('Loss')
plt.title('Loss Evolution During Search')
plt.yscale('log')
plt.grid(True, alpha=0.3)
# For predictions, transform back
y_pred_scaled = model.predict(X_scaled)
y_pred = scaler_y.inverse_transform(y_pred_scaled.reshape(-1, 1)).flatten()
print(f"R² score: {r2_score(y, y_pred):.4f}")
print(f"RMSE: {np.sqrt(mean_squared_error(y, y_pred)):.4f}")
R² score: 0.9999
RMSE: 0.0028
Show code cell source
# Plot comparison
plt.figure(figsize=(10, 4))
plt.subplot(1, 2, 1)
plt.scatter(y, y_pred, alpha=0.5)
plt.plot([y.min(), y.max()], [y.min(), y.max()], "r--")
plt.xlabel("True values")
plt.ylabel("Predicted values")
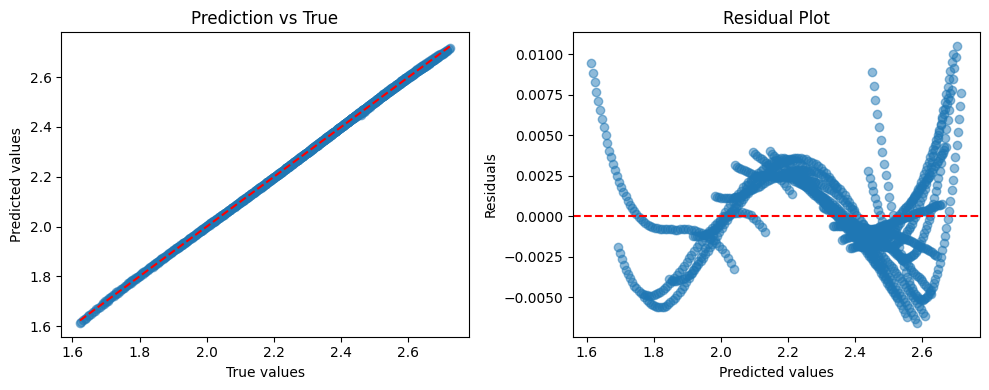
plt.title("Prediction vs True")
plt.subplot(1, 2, 2)
residuals = y - y_pred
plt.scatter(y_pred, residuals, alpha=0.5)
plt.axhline(y=0, color="r", linestyle="--")
plt.xlabel("Predicted values")
plt.ylabel("Residuals")
plt.title("Residual Plot")
plt.tight_layout()
Show code cell source
import numpy as np
import matplotlib.pyplot as plt
wavelengths = ds.wavelength.values
selected_top_widths = ds.top_width.values[::4]
plt.figure(figsize=(10, 4))
plt.subplot(1,2,1)
for tw in selected_top_widths:
if tw in ds.top_width.values: # Only plot if the exact value exists
plt.plot(ds.wavelength, ds.neff_te0.sel(top_width=tw),
label=f"{tw:.2f} µm", linestyle="--", alpha=0.7)
plt.xlabel("Wavelength (µm)")
plt.ylabel("n_eff")
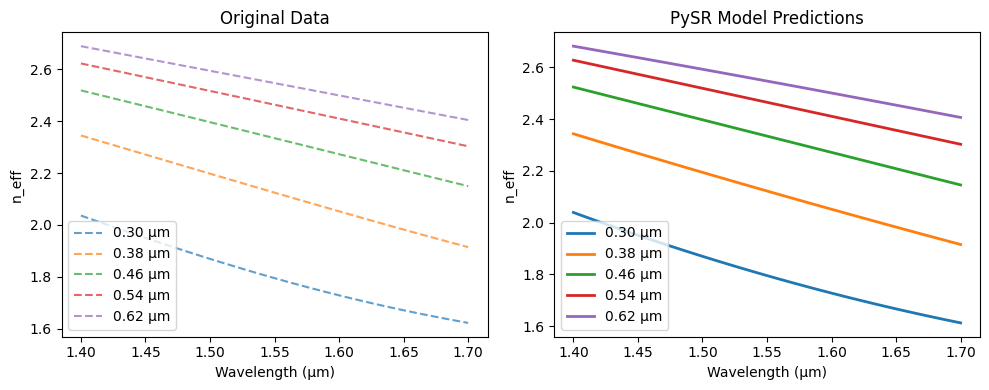
plt.title("Original Data")
plt.legend()
plt.subplot(1,2,2)
for tw in selected_top_widths:
# Create input array for this top_width across all wavelengths
X_pred = np.column_stack([
np.full(len(wavelengths), tw), # constant top_width
wavelengths # varying wavelength
])
X_pred_scaled = scaler_X.transform(X_pred)
y_pred_scaled = model.predict(X_pred_scaled)
y_pred = scaler_y.inverse_transform(y_pred_scaled.reshape(-1, 1)).flatten()
plt.plot(wavelengths, y_pred, label=f"{tw:.2f} µm", linewidth=2)
plt.xlabel("Wavelength (µm)")
plt.ylabel("n_eff")
plt.title("PySR Model Predictions")
plt.legend()
plt.tight_layout()
Show code cell source
# from sympy import symbols
# a = model.sympy()
# a.subs([(symbols("x0"), symbols("w")),
# (symbols("x1"), symbols("λ"))])
# # type(a)
# 1. Get the scaled symbolic expression
expr_scaled = model.sympy()
# 3. Apply inverse y-scaling
y_mean = scaler_y.mean_[0]
y_std = scaler_y.scale_[0]
expr_rescaled = y_std * expr_scaled + y_mean
model.sympy()
\[\displaystyle \left(- x_{0} - \left(x_{0} \left(x_{1} x_{0} \left(0.66593647 - x_{0}\right) \left(-0.007577593\right) - 0.10187686\right) - -0.47428933\right) \left(x_{0} \left(-0.73160255\right) \left(x_{0} - -0.30258545\right) - x_{1}\right) - 0.31943703\right) \left(-0.8628376\right)\]